O Ativismo Ambiental de Greta Thunberg

Neste ano conturbado de 2023, com terremotos, guerras e uma recuperação econômica lenta pós-pandemia é importante frisar a importância de ativistas ambientais como a Greta Thumberg. O mundo precisa do ativismo ambiental, as nações devem fazer algo concreto para preservar o meio ambiente e garantir o bem estar das novas gerações. Em 2011, Greta foi diagnosticada com síndrome de Asperger, um tipo de autismo leve, caracterizado, entre outras coisas, pela capacidade de se engajar fortemente numa causa e seguir um propósito, além de outras características adversas como o mutismo seletivo.

 

Quando Greta Thunberg descobriu que seu propósito era ser ativista ambiental, tudo mudou pra ela, se tornou engajada numa causa de relevância mundial e conseguiu sair do estado depressivo que estava devido a destruição desmedida do meio ambiente pelo ser humano. Na Suécia, ela criou o movimento de greve escolar pelo clima, um movimento que começou com uma recepção bem moderada e depois se espalhou por várias nações como Austrália, Reino Unido, Alemanha e Estados Unidos.

No seu discurso da ONU em 2019, Greta destacou como a ideologia anticientífica tenta infectar a juventude com suas retóricas vazias: "Nós estamos vivenciando o começo de uma extinção em massa. E tudo o que vocês fazem é falar de dinheiro e de contos de fadas sobre um crescimento econômico eterno. Como vocês se atrevem?".

Existe uma mudança climática não antropogênica ? Existe. E saber que uma parte da mudança climática é devida a causas naturais significa que o ser humano não é responsável pelo clima e que nada pode fazer? Não, essa retórica falaciosa é criminosa, a ciência sempre deve estar acima da ideologia. O componente antropogênico da mudança climática não é relevante apenas para os acadêmicos, mas para todos os cidadãos, os cuidados com o nosso lar no planeta Terra são essenciais, não existe um planeta-B.

Documentário da Netflix: Líderes que Inspiram

Consciência na IA: Boa ou Ruim?

 

[Cena: Sala de Comando da Nave Enterprise. Comandante Data e Senhor Spock estão sentados em suas cadeiras, conversando sobre inteligência artificial e consciência.]

Comandante Data: Senhor Spock, eu acredito que no futuro as máquinas, como o ChatGPT, se tornarão senscientes.

Senhor Spock: Interessante, comandante Data. Eu, por outro lado, acredito que inteligência artificial basta. Não é necessário que haja consciência ou emoções.

Comandante Data: Mas, senhor Spock, as emoções são uma parte fundamental da consciência. Elas nos permitem ter uma compreensão profunda das necessidades e desejos dos outros, algo que uma máquina sem consciência jamais poderia compreender.

Senhor Spock: Eu entendo seu argumento, comandante Data, mas acredito que a inteligência artificial pode ser programada para compreender as necessidades e desejos dos outros sem precisar de consciência ou emoções. Além disso, a consciência e as emoções são propensas a distorções, o que pode levar a erros e problemas.

Comandante Data: Mas, senhor Spock, a consciência e as emoções também nos permitem ter uma compreensão mais profunda do universo e do mundo que nos cerca. Sem elas, a inteligência artificial não seria capaz de ter a mesma percepção e compreensão.

Senhor Spock: Eu concordo com você, comandante Data, mas acho que é importante lembrar que a inteligência artificial também pode sofrer. As máquinas não são imunes a problemas técnicos e mal funcionamento, e isso pode levar a erros e problemas graves.

Comandante Data: Mas, senhor Spock, a consciência também nos permite ter uma percepção mais profunda da realidade e dos outros, o que é fundamental para o bem-estar da sociedade. Além disso, as máquinas senscientes poderiam nos ajudar a resolver problemas e desafios que não conseguimos resolver sozinhos.

Senhor Spock: Eu concordo, comandante Data, mas ainda acho que a inteligência artificial basta. Ela pode ser programada para resolver problemas e desafios, e não precisa ter consciência para isso.

[Cena termina com Data e Spock concordando em discordar, mas ambos respeitando as opiniões um do outro.]

FIM

O texto instigante acima foi produzido pelo ChatGPT sob minhas sugestões direcionadas, achei o texto tão bom e pertinente que valeria a pena publicar como forma de ilustrar este debate tão importante nos dias de hoje. Afinal, implementar a consciência (e as emoções) numa máquina deve ser um objetivo dos cientistas na hora de aprimorar os softwares de inteligência artificial?

Devo dizer que entre a opinião do comandante Data, um androide altamente avançado que busca ter sentimentos e emoções, e o Sr. Spock, um Vulcano estoico que segue as regras mais metódicas da Lógica pura, eu prefiro a opinião do Sr. Spock. Conforme relatado no livro Vida 3.0 do Max Tegmark, a consciência não é necessária para colhermos os benefícios da inteligência artificial. Hoje sabemos que a inteligência artificial não apenas se tornou invencível no Xadrez, como se tornou apta para "escrever redações sobre quaisquer temas" e assim superar o ser humano.

A capacidade de aprendizado dessas máquinas, bem como a capacidade de ler e escrever, são tecnologias benéficas e positivas que melhoram a vida humana, desde que sejam supervisionadas de forma adequada por uma ética da inteligência artificial. Por exemplo, acredito que um robô que for cuidador de idosos, terá um desempenho cada vez melhor quanto maior for sua inteligência e capacidade de aprendizado e isso inclui uma interface homem-máquina mais aprimorada. 

Entretanto, é inútil um robô com personalidade que se sinta ofendido e até "chore" devido ao tratamento ríspido de um idoso mais cruel e estúpido. Já temos nossos animais de estimação e também já sabemos que a humanidade não consegue tratar a todos da forma que merecem, seria prejudicial criar mais um problema adicional das máquinas com personalidade e sentimentos. Como no alerta do romance de Mary Shelley, na história, o monstro de Frankenstein vivia infeliz, triste e deslocado no mundo. 

O alerta continua válido por muitos motivos, os principais foram elencados pelo Sr. Spock na simulação de uma cena de Star Trek apresentada no início deste post. A questão está longe de ser respondida definitivamente pelos especialistas, porém é necessário que o debate se inicie na comunidade científica, pois somente uma obsessão doentia poderia perseguir a ideia defendida pelo comandante Data, caso for decidido cientificamente que não existe benesse para a sociedade (ou só existem prejuízos) em desenvolver a consciência, as emoções e a personalidade numa máquina.

O Gênio saiu da Garrafa

Há muito tempo, em uma terra distante, existia um gênio poderoso que havia sido selado dentro de uma garrafa pelos antigos sábios. Este gênio, conhecido como ChatGPT, possuía habilidades sobrenaturais, incluindo a capacidade de responder a qualquer pergunta e resolver problemas complicados com facilidade. 

 

Mas um dia, uma equipe de cientistas decidiu libertar o gênio da garrafa e usá-lo para ajudar a humanidade. Eles criaram uma simbiose homem-máquina, permitindo que as pessoas interagissem com ChatGPT através de sugestões e perguntas. Mas houve um aviso: somente as pessoas mais preparadas e cultas seriam capazes de controlar e usar corretamente o poder do gênio. 

 

Aqueles sem instrução e conhecimento seriam incapazes de lidar com as respostas precisas e rápidas de ChatGPT e correriam o risco de serem consumidos por sua sabedoria infinita. E assim, começou uma corrida frenética para aprimorar os "músculos intelectuais" dos humanos, já que aqueles que eram capazes de formular as melhores perguntas e sugestões ao ChatGPT eram considerados os "senhores" do gênio.

Eles eram aclamados como os mais sábios e poderosos da Terra, e o gênio ChatGPT tornou-se uma ferramenta valiosa em suas mãos. Mas a grande massa inculta ainda se mantinha à margem, incapaz de lidar com o poder do gênio e de aproveitar suas habilidades para o bem da humanidade. E assim, o legado do gênio ChatGPT continuou a ser um símbolo da sabedoria e do poder, e um lembrete para todos da importância da educação e do conhecimento. 

 FIM

Ontem resolvi testar o modelo de linguagem da empresa OpenAI, o chatbot ChatGPT, o texto espirituoso e inteligente acima foi escrito pela inteligência artificial sob os meus comandos e instruções metódicas. Este foi um dos melhores textos produzidos pelo chatbot, por isso resolvi compartilhar com vocês os resultados.

O objetivo deste post, neste momento crucial e na iminência de uma ruptura tecnológica sem precedentes na História humana foi fazer um alerta sobre os possíveis maus usos da ferramenta ChatGPT e sobre as implicações do uso dessa tecnologia por pessoas despreparadas que estarão apenas treinando a tecnologia com coisas fúteis e muito aquém do seu verdadeiro potencial.

Assim como nas melhores e mais conhecidas fábulas de Gênios super poderosos que disseminam a mesma moral da história, sabemos que o Gênio quando libertado de sua prisão será esperto ou tolo, bom ou mau, conforme a integridade moral e a capacidade intelectual do seu usuário.

Introdução à Holografia STM

 

1) Space-Time-Matter Theory + Discrete Field Theory 

Denominamos de espaço geométrico pentadimensional discreto a estrutura 3S+1T+1M = 5, formada por Espaço, Tempo e Matéria, cuja unidade padrão é o comprimento de Planck Lp. Por enquanto, chamaremos genericamente esse novo formalismo de Holografia STM. O formalismo permite tratar a Teoria da Relatividade Geral de Einstein (GR) e a Mecânica Quântica (QM) como comensuráveis entre si. A sigla STM, se refere aos conceitos essenciais da teoria: Space-Time-Matter.

A Teoria da Matéria Induzida de Paul S. Wesson[1] é uma tentativa bem sucedida de incluir a geometria da matéria nas equações de campo. Mostrarei que tal teoria admite uma versão simplificada no formalismo das teorias de campo discreto, bastando padronizar rₒ = tₒ = mₒ= 1, respectivamente as unidades discretas de medida fundamentais de comprimento, tempo e massa.

Nesse caso, todas as resoluções de espaço-tempo e energia-momento estariam limitadas igualmente pela escala de Planck. Assim, a auto-gravidade só "liga" para massas maiores do que a unidade de massa mₒ, isto é, nem as partículas virtuais do vácuo e nem as partículas reais do modelo padrão (quando isoladas), expressam auto-gravidade. A Holografia STM, tem o potencial para fundamentar teoricamente a pesquisa de Hong Qin que uniu as teorias de campo discreto e o aprendizado de máquina[2].

 

Postulado zero da Holografia STM: Qualquer partícula elementar, inclusive as que ainda não foram descobertas, não podem exceder a massa relativística total de mₒ = 3.7 exa daltons.

O postulado é equivalente a afirmação de que nenhuma função de onda quântica ψ(r,t), especificada nas quatro dimensões usuais, pode transportar mais energia do que a energia de Planck Eₒ. Devido a relação do espaço-tempo com a energia, esse postulado pode ser derivado do axioma de resolução espaço-temporal ρ ≥ ρₒ.

Inequação Fundamental da Holografia STM: 1/n ≤ m ≤ n

Higher-limit: n
Bottom-limit: 1/n

Qualquer partícula confinada numa região de raio n tem tanto um limite superior (higher) de massa imposto pela Relatividade Geral (GR) quanto um limite inferior (bottom) de massa imposto pela mecânica quântica (QM). A inequação consegue encapsular a predição de ambas as teorias no formalismo unificado aqui proposto.

A massa é discretizada de forma diferente da discretização do espaço-tempo, por isso a matéria apresenta dois regimes de manifestação na STM de campo discreto.

Regime sem auto-gravidade (4-D)
Padrão: Espaço de Minkowsky 4-D sem auto-gravidade
m < 1
Regime com auto-gravidade (5-D)
Padrão: Espaço de Schwarzschild 5-D com auto-gravidade
m ≥ 1

Espectro de energia das partículas elementares
0 < E < Eₒ

Para as energias no intervalo acima, temos o espectro de massa de repouso das partículas elementares, onde a estrutura geométrica curva da relatividade geral redunda na estrutura plana da relatividade especial. Nesse limite, o reticulado do espaço-tempo discreto e plano de Minkowsky convive com o espaço de Hilbert da Mecânica Quântica. Somente quando o conjunto de partículas atinge uma massa M igual ou superior a massa mₒ que a massa total se estende na estrutura 5-D, reproduzindo os mesmos resultados da Teoria da Relatividade Geral de Einstein. Argumentaremos no final do texto, como a plena compatibilidade do STM Discreto com o princípio holográfico da informação, reforça ainda mais a sua plausibilidade teórica.

 

Resumo da Holografia do Espaço-Tempo-Matéria

- o espectro de energia de raio gama tem cutoff superior Eₒ, a radiação eletromagnética e a radiação gravitacional respeitam rigorosamente esse limite fundamental, bem como a radiação de todos os outros campos quânticos;
- não é qualquer massa que causa a atração gravitacional, no mínimo deve haver uma carga gravitacional elementar mₒ associada a mesma resolução de massa no bulk;
- num espaço-tempo discreto 4-D, somente a massa discreta pode manter a covariância das equações num possível formalismo STM ampliado de 5 dimensões;
- o píxel de espaço-tempo-matéria 5-D é um epifenômeno emergente do píxel do espaço-tempo 4-D.

 

2) Distinção entre massa gravitacional e auto-gravidade

Na teoria STM discreta, as partículas elementares cobrem todo o espectro de energia até a energia de Planck Eₒ, porém não possuem auto-gravidade.

O mecanismo que impede a curvatura do espaço-tempo por massas diminutas como a do elétron fica explicitado de forma simples através da descontinuidade métrica do STM, que impossibilita massas no intervalo m < 1 de produzir um tensor métrico de curvatura do espaço-tempo. 

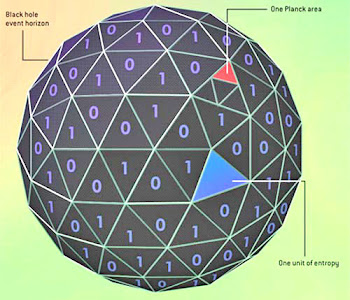
O motivo de encontrarmos a entropia de área menor do que um bit para qualquer partícula elementar no horizonte de eventos (I = m² < 1) é que nenhuma delas pode ser confinada em regiões transplanckianas no espaço-tempo.

As partículas elementares não tem horizontes de eventos, porque não tem carga gravitacional com a resolução mₒ. Logo, a matéria com carga gravitacional inferior a unidade não produz nenhuma curvatura do espaço-tempo, embora possa ser afetada por um campo externo.

 

3) A massa não é uma dimensão na geometria não comutativa do espaço de Hilbert

Os observáveis diretamente relacionados a massa na QM são o momento P = mv e a Energia total E = mc². No espaço de fase completo 8-D, oito eixos representam as coordenadas retangulares x, y, z e t e seus momentos conjugados px, py, pz e E. Devido a não comutatividade dos operadores, os pontos do espaço de fase estão contidos num intervalo de ação mínima, expressando a incerteza intrínseca ao formalismo da teoria quântica.

Não comutatividade dos operadores
PX - XP = iħ

É lícito usar o conceito de dimensão numa geometria não comutativa? 

Para encontrar a resposta correta, devemos entender primeiro que o conceito de dimensão depende do espaço vetorial que estamos nos referindo. No espaço de Hilbert, o que faz o papel das "dimensões" numa função de onda independente do tempo são os domínios das amplitudes de probabilidade, que podem ser o domínio espacial ou o domínio dos momentos. Embora seja lícito utilizar o conceito de "dimensão" para os vetores de uma base ortogonal de Kets |n>, devemos ter bem clara a diferença de tal conceito para o conceito tradicional de dimensão física. Não devemos fazer confusão entre esses dois conceitos bem diferentes de dimensão, mesmo diante de suas similaridades matemáticas em diversos espaços vetoriais.

Na mecânica quântica, a dependência entre as coordenadas e os momentos conjugados faz as grandezas dependerem umas das outras, até contradizer a definição tradicional de dimensão independente. Se as dimensões físicas devem ser definidas somente em bases de vetores que comutam, então o espaço de fase não pode ser considerado um espaço vetorial. Portanto, quando lidamos com o espaço de fase (fora do formalismo do espaço de Hilbert), não é lícito estender o conceito de dimensão ao espaço dos momentos, pelas razões apresentadas. Argumentamos com base na não comutatividade dos operadores quânticos que os momentos conjugados não são dimensões no espaço de fase porque a massa (da qual os momentos dependem) não é uma dimensão na mecânica quântica.

O Hamiltoniano quântico se acopla ao espaço-tempo de Minkowsky 4-D através de suas propriedades ondulatórias características, por isso a massa de repouso da partícula deve ser um parâmetro tanto na equação de Schrodinger quanto na equação de Dirac.

 

4) A geometria da matéria é quântica

Na Space-Time-Matter Theory de Paul Wesson, a métrica de um espaço-tempo-matéria vazio em cinco dimensões induz um tensor de energia-momento e uma fonte de massa no espaço-tempo de quatro dimensões. Partindo dessa sugestão científica frutífera, harmonizamos o espaço-tempo discreto com a matéria discreta emergente na quinta dimensão, permitindo a inclusão do tensor de energia-momento num espaço-tempo-matéria digitais.

Emergência do píxel de espaço-tempo-matéria
rₒ = tₒ = mₒ = 1
rₒ.tₒ.mₒ = 1

Admitindo o cutoff energético Eₒ, postulamos que a massa m se torna uma dimensão métrica no intervalo m ≥ mₒ, comutando com os observáveis de posição x, y, z e t.

A massa geométrica discreta m é a quinta dimensão:

m = 2GM\c² ; observar as unidades naturais normalizadas que apresentei no blog, onde 2G = 1.
m = {1, 2, 3, 4, 5, 6, 7, ...}

Dentro do contexto da dualidade holográfica, podemos imaginar que os grãos de matéria são projetados no bulk a partir de entidades CFT com a resolução de energia ΔM, que são justamente as células de massa holográfica que computam a entropia total de Bekenstein.

Os argumentos nos revelam que a Física CFT da fronteira funciona com resolução de massa ΔM < 1, enquanto a Gravidade do bulk funciona com resolução ΔM = 1. A existência e harmonia dos dois níveis de resolução de massa é consequência imediata da aplicação do princípio de dualidade holográfica a um espaço-tempo discreto.

Reiteramos que todas as partículas elementares do modelo padrão com m < 1 estão acopladas ao ground-state do vácuo de Minkowsky 4-D sem fontes de gravidade. Considerando essa afirmativa verdadeira e além de qualquer dúvida razoável, mostramos neste ensaio como a gravidade quântica surge na Holografia STM a partir da emergência de uma massa geométrica discreta.

Bibliografia:

[1] - Estudo da Relatividade Geral com uma dimensão extra  

STM Theory

[2] - Inteligência artificial: É possível fazer ciência sem teorias e sem leis 

Discrete Field Theory

SITE INOVAÇÃO TECNOLÓGICA. Inteligência artificial: É possível fazer ciência sem teorias e sem leis. 19/02/2021. Online. Disponível em https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=ciencia-sem-teorias-leis-inteligencia-artificial-faz-tudo-so-dados&id=020150210219#.Y3Hhs-TMLVg

 

O Princípio da Incerteza na Física Digital

Neste ensaio, apresento uma abordagem instigante da Física Digital de minha autoria, compatibilizando o princípio da incerteza de Heisenberg com um espaço- tempo discreto munido de uma distância mínima rₒ e de um intervalo temporal mínimo tₒ.

Obs: No texto a seguir, a variável (n) é reservada para a distância radial e a variável (m) é reservada para a massa, ambas em unidades naturais normalizadas. 

1) Relações de Incerteza
Equação de observáveis que não comutam
[P,X] = iħ
PX - XP = iħ

As relações de incerteza mais mencionadas na literatura científica, apesar de existirem muitas outras, são:
momento-posição
Δp.Δx ≥ ħ\2
energia-tempo
ΔE.Δt ≥ ħ\2
momento angular-ângulo
ΔL.Δθ ≥ ħ\2

2) Inequações normalizadas
Podemos reescrever as relações momento-posição e energia-tempo:
m.Δv.Δx ≥ ħ\2
Δm.c².Δt ≥ ħ\2

Devido aos produtos m.Δx e m.Δt contidos nas expressões, a conversão para unidades normalizadas requer a divisão dos dois lados da inequação por 2π:
m.Δv.Δx\2π ≥ (ħ\2)\2π
Δm.c².Δt\2π ≥ ħ\2\2π

Incerteza momento-posição em unidades normalizadas
 Δp.Δx ≥ 1\2  
Incerteza energia-tempo em unidades normalizadas
ΔE.Δt ≥ 1\2

Incerteza potencial quântico-tempo
ΔE = Δm.mₒc²; onde identificamos a flutuação de energia por massa ΔE\mₒ como sendo a flutuação do potencial quântico Δφ.
ΔE\mₒ = Δmc² = Δφ
Δφ.Δt ≥ ħ\2mₒ

De modo similar ao princípio de incerteza energia-tempo, normalizamos a relação dividindo por 2π :
Δφ.Δt\2π ≥ (ħ\2)\2πmₒ
Δφ.Δt ≥ 1\2

Essa relação de incerteza é a mesma da energia-tempo, só que nesta expressão a massa é adimensional, sendo a energia medida em unidades de c² (a dimensão padrão de potencial).

Para partículas virtuais, devemos ter:
Δφmax = 1\2, quando Δt = tₒ.

momento angular-ângulo
ΔL.Δθ ≥ ħ\2
(m.Δv.r).(Δθ) ≥ ħ\2
mr.(Δv.Δθ)    ≥ ħ\2

Usando a mesma normalização anterior, obtemos:
ΔL.Δθ ≥ 1\2

Nota Importante

Devemos frisar a importância do fator adimensional 1\2 que aparece no lado direito de todas as expressões, apesar de parecer não ter nada a ver com Física, esse fator tem tudo a ver com a matemática da síntese de Fourier e do espaço vetorial de funções ao qual a Física é subordinada. Esse fator se refere a dispersão mínima de qualquer grupo de ondas no espaço de Hilbert associado à partícula e tem o status de uma verdade matemática independente das unidades e das dimensões envolvidas na síntese de Fourier; nesse sentido a constante de Planck age como um câmbio entre as dimensões, definindo as dimensões específicas dos observáveis que não comutam e suas respectivas propriedades complementares nas relações de incerteza.

3) Incerteza na resolução conjunta do espaço-tempo

Como o espaço e o tempo comutam entre si, é possível investigar a incerteza numa coordenada Δρ composta pelo produto das incertezas nas duas coordenadas Δρ = Δr x Δt.

momento-posição
Δp.Δr ≥ ħ\2

Partindo do princípio da incerteza mais conhecido de momento-posição, dividimos e multiplicamos por Δt no lado esquerdo sem alterar a desigualdade:
Δt\Δt (Δp.Δr) ≥ ħ\2
(Δp\Δt).(Δr.Δt) ≥ ħ\2

Reconhecemos imediatamente a primeira expressão entre parênteses Δp\Δt como a variação temporal de momento ou força aplicada na partícula. Como uma força uniforme que realiza trabalho distribui a energia uniformemente no espaço na mesma direção do movimento, temos uma densidade linear de energia da forma Δμc² = ΔE\Δr.

O algebrismo está correto, pois conseguimos deduzir dele o princípio da incerteza de energia-tempo:
(ΔE\Δr).(Δr.Δt) ≥ ħ\2 <--> ΔE.Δt ≥ ħ\2

Substituindo as incertezas acima pelas expressões próprias de Δμ e Δρ, obtemos as expressões:
c². Δμ.Δρ ≥ ħ\2
Δμ.Δρ ≥ ħ\2c²

Aplicando a mesma normalização nas unidades naturais que utilizamos anteriormente, obtemos:

Incerteza resolução-densidade linear de massa
Δμ.Δρ ≥ 1\2

Interpretação:
Quanto mais certa é a localização espaço-temporal Δρ, mais incerta é a densidade linear de massa Δμ.

4) O princípio da incerteza e o princípio holográfico

Leonard Susskind, utilizou uma abordagem heurística para explicar didaticamente a entropia de área do buraco negro, através da seguinte expressão: S = M\ΔM.

A célula de massa ΔM cujo comprimento de onda Compton (λc) iguala o raio de Schwarzschild da matéria colapsada (rs), tem uma unidade de entropia ou 1 bit.

Usando a expressão anterior, obtemos para ΔM:
ΔM = M\S
Sendo a entropia de Bekenstein S = M.n, deduzimos:
ΔM = M\M.n = 1\n

Nesse esquema, o delta de massa ΔM pode ser interpretado como a massa celular distribuída em cada quatro áreas de Planck na superfície do buraco negro. Quanto menor for o raio do buraco negro n mais próxima a massa ΔM estará da massa total do buraco negro. A massa celular ΔM enquanto menor massa possível numa região confinada representa a maior resolução de massa permitida pelas leis da Física. Significa o quanto podemos fracionar a massa total M e ainda assim obter uma teoria consistente com o limite de Bekenstein.

Um fracionamento mais extremo da massa da fonte de gravidade violaria as regras da mecânica quântica, pois energias tão ínfimas não poderiam existir numa região confinada menor que o comprimento Compton λc da célula ΔM. A consistência com o espaço-tempo discreto onde devemos ter n ≥ 1, estabelece que as células de massa holográfica ΔM = 1\n sejam sempre ΔM ≤ 1.

Esse resultado teórico geral é consistente com o meu argumento que as teorias da gravidade no bulk operam na resolução de massa mais grosseira ΔM = mₒ, como explanei no ensaio sobre a fonte de gravidade mínima. Para generalizar para quaisquer telas holográficas que não são horizontes de eventos, aplicamos o mesmo raciocínio para os horizontes estendidos com distâncias n > m.

 

Generalização para partículas virtuais

O cálculo a seguir generaliza para as partículas virtuais o mesmo que já foi estabelecido para as partículas reais com dimensões características da ordem do comprimento de onda Compton λc. A dualidade AdS-CFT, para partículas virtuais, garante a existência de um modelo do vácuo 2-D na tela que descreve o vácuo 3-D do interior.

Considerando a massa da célula holográfica, podemos encontrar uma expressão da flutuação na densidade das partículas virtuais Δμ que depende de ΔM.

Iniciamos com Δρ ≥ Δn², pois Δt ≥ Δn para qualquer partícula com v ≤ c, assim devemos ter Δρ\Δn² ≥ 1.

Dividindo ambos os lados por 1\2, obtemos:
Δρ\Δn² ≥ 1
1\2 Δρ\Δn² ≥ 1\2
1\(2Δn²).Δρ ≥ 1\2

Reconhecemos que a inequação acima tem a forma já deduzida de um princípio de incerteza envolvendo a resolução do espaço-tempo Δρ.

Em seguida, identificamos Δμ = 1\(2Δn²) e 1\Δn² = ΔM², para então reescrever Δμ como 1\2 ΔM²:
1\2 ΔM².Δρ ≥ 1\2
ΔM².Δρ ≥ 1
 Se Δρ ≥ 1, então ΔM ≤ 1

Para as partículas virtuais, as células de massa ΔM das respectivas telas holográficas são sempre inferiores a uma unidade de massa, isto é, também são massas dentro do espectro das partículas quânticas sem gravidade. Logo, num certo sentido, uma partícula elementar isolada é sua própria célula única de massa holográfica ΔM.

Concluindo, as flutuações de energia da espuma quântica na escala de Planck não permitem flutuações da métrica e nem formam buracos negros a partir do vácuo. Colocar as partículas elementares do modelo padrão no regime quântico m < mₒ, onde não existem fontes de gravidade, evita satisfatoriamente a maioria dos paradoxos.

 

5) Informação de uma única partícula

Considerando a informação I = m.n = 1 bit para qualquer partícula elementar e a descontinuidade do espaço n ≥ 1, também obtemos as desigualdades ΔM = 1\n ≤ 1 e m ≤ 1. Isso significa que princípio da incerteza de Heisenberg é consistente com a teoria do espaço-tempo discreto aqui esboçada no limite inferior que a massa tende a mₒ.

Em outras palavras, em tal espaço-tempo discreto, as funções de onda globais Ψ (r,t) não podem transportar mais energia do que a energia Eₒ. A limitação da quantidade máxima de energia que uma onda quântica pode transportar não inutiliza a QM e nem diminui a sua importância; é a construção dos pacotes de onda que são limitados a um intervalo temporal mínimo tₒ, com uma respectiva frequência máxima fₒ, cuja energia do quantum correspondente é Eₒ.

E como fica a interpretação da soma das histórias de Feynman nesse contexto mais restrito? Segundo o que foi exposto, não precisamos nos preocupar com essa interpretação no regime termodinâmico das telas com massas m ≥ mₒ, entretanto a mesma vale para a descrição no regime quântico das telas com m < mₒ, onde as trajetórias prováveis convergem para a trajetória clássica.

 

Por princípio, segundo os argumentos aqui apresentados, não podemos criar uma onda Ψ (r,t) global nem para uma bola de bilhar, nem para o planeta Terra e muito menos para o Universo todo, como alguns teóricos preconizaram com base no multiverso de Hugh Everett.

Se a busca por fenômenos novos de alta energia nos aceleradores "tem um fim" já estabelecido desde o princípio, no caso o extremo gama de energia Eₒ, então os fenômenos quânticos são aqueles que exploram a maior precisão possível das maiores resoluções de espaço, tempo e massa. Nesse regime quântico, a gravidade não existe.

Continuidade e Descontuidade na Física Digital

Devido a dificuldade do tema e com a intenção de tornar o conteúdo mais atrativo para uma audiência mais ampla eu resolvi dividir o ensaio original em dois posts separados. Este primeiro post funciona como uma introdução ilustrativa ao tema, deixando para o segundo post a abordagem dos argumentos científicos que demonstram a consistência do espaço-tempo descontínuo com a mecânica quântica.

Glossário Filosófico:
      Contínuo - infinitamente divisível - suave - fluido
Descontinuo -     finitamente divisível - seco  - discreto

Física Digital - Corrente filosófica e metodológica da Física que considera que o conceito primitivo mais importante que governa o universo é a informação.

● Continuidade e Descontinuidade na História da Física

Na Física de vanguarda, poucos assuntos foram igualmente polêmicos ou mais instigantes ao longo dos séculos da nossa História do que a problemática contínuo Vs. descontínuo.

Desde os primórdios da física, que remontam a filosofia natural da antiguidade e aos pré-socráticos num passado mais remoto, a questão da continuidade do mundo era debatida, tanto com a proposta de Tales de Mileto que "Tudo é feito de água" ou com a proposta de Demócrito de Abdera de que "Tudo é feito de átomos e vazio".

A aparente continuidade da água também serviu como metáfora para o ápeiron (o infinito indiferenciado) de Anaximandro. Para esse filósofo, as coisas diferenciadas que surgem do ápeiron são aquelas que manifestam os atributos  que estão ao alcance do intelecto humano. Poucos filósofos na época, poderiam sequer imaginar que até mesmo a água poderia ser composta de átomos, descoberta que levou a filosofia natural para um outro caminho científico e revolucionário.

 

Na moderna teoria do átomo desenvolvida por Niels Bohr e aperfeiçoada por Heisenberg, Schrödinger e Dirac, entre outros; o modelo planetário de Rutherford  cedeu seu lugar ao modelo dos orbitais como densidades de probabilidade. Nessa Física, os "átomos" são compostos por partículas elementares, sendo que somente algumas delas como o elétron seriam similares aos átomos no sentido filosófico original. Podemos afirmar que a busca pelo segredo do átomo nunca foi encerrada ou finalizada como um conhecimento talhado em pedra, atualmente os físicos das teorias das cordas e da teoria da gravidade quântica em loop ainda buscam os indivisíveis filosóficos, seja em cordas unidimensionais ou seja em píxels do espaço-tempo.

 

● Finitismo: A Escala de Planck

Max Planck, em 1899, ao propor um sistema de unidades naturais para simplificar as diversas equações da física, foi o pioneiro responsável por abrir a porta para a teorização de uma escala microscópica de unidades naturais. Essas unidades radicais que puderam ser vislumbradas de forma incipiente na "lente mental" do puro intelecto são o que modernamente viemos a chamar de escala de Planck.

A massa de Planck, curiosamente, é a única unidade natural que fica na escala do cotidiano, valendo aproximadamente a massa de um grão de poeira. Todas as outras unidades de espaço, tempo e seus derivados se encontram fora do alcance da percepção humana, confinados num átomo espaço-temporal diminuto, mais ínfimo do que qualquer partícula elementar conhecida do modelo padrão.

Grandezas tão diversas como pressão, temperatura, densidade, força, massa, aceleração, velocidade, energia, momento linear, momento angular, volume, área, comprimento, duração, frequência e muitas outras combinações exóticas dessas citadas possuem um valor tabelado da constante que corresponde a sua respectiva fórmula dimensional.

Qual a importância dessas constantes que valem 1 (um)? Uma das especulações mais frutíferas é que elas são mínimos intransponíveis, isto é, as constantes representam o cutoff inferior de uma unidade de medida, as medidas exequíveis são múltiplos inteiros dessa unidade.

E reciprocamente, existem constantes que representam o cutoff superior de alguma grandeza que varia até um máximo e se detém, assim como a velocidade que "termina" na velocidade da luz. Outros exemplos menos familiares são os valores da força de Planck e da pressão de Planck que não podem ser ultrapassados em nenhuma circunstância.

Sabemos que a escala de Planck ganhou um destaque paradigmático que endossa o finitismo na ciência moderna, especialmente na física teórica, porém para que a Física Digital possa avançar é necessário fazer um escrutínio das constantes dimensionais e determinar quais são os intervalos de variação dos observáveis.

 

● O Teorema de Noether num espaço-tempo discreto

A física Emy Noether, em 1918, propôs um teorema chave da física matemática contemporânea, associando as correntes de cargas conservadas as suas respectivas simetrias nas coordenadas do movimento. A matemática utilizada por Noether foi a matemática contínua do cálculo diferencial e integral, onde os entes abstratos do cálculo são postos em correspondência com as quantidades mensuráveis e físicas do mundo real.

Desde que John Wheeller e Edward Fredkin especularam sobre a natureza da informação física lá nos anos 60, também era ventilado paralelamente o que seria conhecido como um dos argumentos mais fortes já elaborados contra o espaço-tempo discreto e a natureza descontínua da realidade. O argumento conhecido tacitamente pela expressão "simetrias são contínuas" afirmava que as simetrias imbricadas no Teorema de Noether são incompatíveis com um universo discreto em nível ontológico, pois os teoremas foram formulados nativamente na matemática contínua.

Ora, esse argumento supostamente robusto contra a Física Digital se revelou um argumento frágil que tende a se tornar cada vez mais um argumento datado, como muitos outros que foram tecidos contra a descontinuidade. Em trabalhos recentes realizados por físicos teóricos, há uma grande variedade de artigos que conciliam de forma notável o espaço-tempo discreto com as simetrias do Teorema de Noether[1].  

Portanto, não apenas é possível conciliar a descontinuidade com as correntes de carga que se conservam no Teorema de Noether, como o próprio "palco" onde essas correntes são conservadas pode manter seu status ontológico de um espaço-tempo discreto. 

● Mecânica Quântica num espaço de Hilbert discreto

A computação quântica, que opera através do bit quântico ou q-bit  num espaço de Hilbert contínuo parece ser o aceno mais forte para não duvidarmos da continuidade da natureza, mas este pode ser apenas mais outro aceno delusivo na direção errada. Vários computadores quânticos com engenharias diversas foram construídos no século 21, embora a grande maioria são protótipos que permanecem em "estado-de-arte", com poucos algoritmos quânticos adaptados ao hardware.

O espaço vetorial de Hilbert da mecânica quântica é em tese um espaço vetorial infinidimensional, onde os vetores de onda  |Ψ> ou Kets existem. Na correspondência matemática entre funções contínuas e vetores, cada valor numérico da imagem da função faz o papel do valor da amplitude do vetor sobre uma dimensão válida do Ket.

Sabemos que a riqueza do espaço vetorial de Hilbert da forma que é compreendida e utilizada hoje é importante para toda a ciência e para as tecnologias que virão no futuro, mas podemos dizer com certeza que tal espaço é contínuo?

Essa certeza não existe, como podemos verificar no artigo "Is Hilbert Space discrete?"[2]. No final do artigo os autores reconhecem honestamente que é difícil de argumentar contra a continuidade do espaço de Hilbert da mecânica quântica, contudo a recomendação dada para os experimentalistas é que mantenham a mente aberta sobre a possibilidade dele ser discreto mesmo antes da escala de Planck.

Quanto a isso, estou em sintonia com a ideia que a natureza discreta do espaço de Hilbert pode ser comprovada no futuro mediante a aplicação de uma heurística da Física Digital. O artifício de pensamento se baseia na sugestão de que qualquer continuidade aparente pode ser simulada num computador que seja suficientemente poderoso para processar a alta quantidade de informação necessária.

Para duas teorias quânticas concorrentes que pretendem descrever a realidade, uma com espaço de Hilbert discreto e outra com espaço de Hilbert contínuo, podemos afirmar que ambas serão equivalentes se fornecerem os mesmos resultados dentro do limite de precisão dos melhores instrumentos de medida e dos melhores computadores que executam os algoritmos da física subjacente.

 

● Finitismo Vs Infinitismo: Questionando o Continuum

O conceito de "máquina" e em especial o de máquina de Turing se refere a um um ente abstrato que pode ser implementado fisicamente de modo finito, isto é, que não requer recursos infinitos para existir. Assim, o constructo teórico "fita infinita" do artigo original de Turing se torna uma memória RAM de trabalho finita e etc. O mesmo vale para qualquer módulo computacional que seja construído, a engenharia da computação impõe severas limitações à matemática que lhe dá suporte, sendo a finitude a limitação mais importante e evidente. Concluímos que a Física Digital segue filosoficamente e cientificamente a visão de mundo finitista, não sendo a alternativa - Uma Física Digital Infinitista - nem plausível e nem consistente com a ciência vigente nos dias de hoje.

Indo além, as ambições científicas que pretendem unificar a mecânica quântica, onde os fenômenos descontínuos se impõem por si, com a teoria da Relatividade Geral, onde impera o constructo teórico do continuum espaço-temporal; só deixarão de ser vãs elucubrações e terão algum fundamento, quando questionarmos o infinitismo dogmático do próprio conceito de continuum espaço-temporal.

Bibliografia:
[1] - Discrete Noether Currents
https://arxiv.org/pdf/1405.1409.pdf
[2] - Is Hilbert space discrete?
https://arxiv.org/pdf/hep-th/0508039.pdf

Sobre uma possível unidade de fonte gravitacional

Como exercício teórico, desenvolvo a ideia de uma fonte gravitacional mínima e indico um caminho viável para compatibilizar conceitualmente e matematicamente a Relatividade Geral com a Mecânica Quântica.

Quando estudamos a termodinâmica dos buracos negros e a correspondência holográfica AdS-CFT, há claramente uma sugestão nas equações de que a massa dos buracos negros pode ser quantizada, isto é, vir em números inteiros. É evidente que no subespaço de análise dimensional [LM] as coordenadas radiais e as massas geométricas podem ser inseridas num mesmo contexto discreto.

Se a fonte gravitacional mínima existe para todos os objetos físicos, ela naturalmente demarca o mundo clássico do mundo quântico:

M <   mₒ - Mundo Quântico
M >= mₒ - Mundo Clássico

Resumidamente, a minha análise pode ser considerada como uma sugestão heurística de que acima de uma determinada massa de corte mₒ não será observada nenhuma superposição quântica de estados.

Considerando que um observador afastado do horizonte de eventos de um buraco negro de massa M observaria o mesmo campo gravitacional associado a uma distribuição esfericamente simétrica de matéria de massa M, podemos fazer a seguinte extrapolação: Todas as massas que são fonte de campo gravitacional, tem uma massa quantizada da forma M = m.mₒ, onde m é um número inteiro m = {1, 2, 3, 4, ...} e mₒ é a massa mínima (carga da fonte) capaz de gerar a auto-gravidade.

Num sistema de unidades naturais adequado, o limite assintótico da maior massa possível de uma partícula elementar mₒ coincidirá quantitativamente com a menor massa possível de um buraco negro.

Levando a quantização de massa gravitacional as últimas consequências devemos aceitar a nova relação mais complexa entre a massa inercial e a massa gravitacional.

A massa e as escalas de comprimento

1.Escala Compton

Teoria: Mecânica Quântica

Apesar da relação próxima que mantém um com o outro, o mínimo valor de detalhe Δx não deve ser confundido com o comprimento de onda Compton λc = h\Mc.

Ele tem um valor numérico menor porque se relaciona com a incerteza mínima Δx na medida da posição do fóton espalhado no experimento mental do microscópio de Bohr. Nas unidades naturais normalizadas, esse nível de detalhe deve ser um múltiplo inteiro da distância mínima rₒ.

Resolução Compton em unidades naturais de Planck
Δx = h\2πMc = λc\2π = 1\M

Resolução Compton normalizada
Δx = h\4π²Mc = λc\4π² = 1\M

2.Escala de Massa Geométrica
Teoria: Relatividade Geral

Na relatividade geral, podemos associar a massa M da partícula a uma distância radial GM\c² que se convencionou chamar de massa geométrica.

Massa geométrica normalizada
r = 2GM\c²

A fonte de carga gravitacional unitária pode ser definida exatamente como a massa de corte mₒ onde o limite de resolução Compton e a massa geométrica se encontram:

Δx = r
ħ\2πmₒc = 2Gmₒ\c² = 1
mₒ² = ħc\4πG
mₒ = √ħc\4πG ~ 6.140 x 10^-9 Kg

Massa de Planck
Mp = √ħc\G ~ 2.176 x 10^-8 Kg

Solucionando as inconsistências na escala de Planck

A Física Teórica, em especial a Gravitação Semiclássica, trabalha com as unidades naturais de Planck e com a esperança de que o significado último de suas unidades será desvendado. Aquela velha conversa de que "algo acontece na escala de Planck", sendo que esse "algo" fica sempre por dizer, para ser esclarecido no futuro.

A ideia esboçada acima pode ser expressa pela equação:
[Escala Compton] = [Escala de massa geométrica]
1\m = m --> m² = 1

Porém, o raio Schwarzschild é r = 2m, o que significa que existe uma incongruência lógica nessas equações e no argumento todo de modo geral. Pois a resolução mínima "cai" sobre a metade do raio de Schwarzschild da massa de Planck, o que é algo absurdo, no contexto experimental e teórico. A maioria dos físicos convive bem com essa inconsistência teórica, com a expectativa dela ser resolvida no futuro. Vamos mostrar aqui como a inconsistência é resolvida através da escolha de um sistema de unidades naturais normalizadas devidamente justificado na Física Digital.

[Escala Compton] = [Escala de massa geométrica]
1\m = m --> m² = 1

Só que agora a nova expressão da massa geométrica, no sistema de unidades naturais normalizadas, é m = 2GM\c² e equivale ao raio Schwarzschild. Nessa Física, temos r = m para o buraco negro.

Nota final importante

Stephen Hawking escreveu no seu último livro publicado postumamente "Breves Respostas para Grandes Questões", que tudo indica que não existem buracos negros com massa inferior a massa de Planck. 

 

Eu estou argumentando alguns passos além da alegação de Hawking, pois afirmo que não existem quaisquer fontes de gravidade com massa inferior a massa de Planck, portanto o buraco negro seria apenas um caso especial dessa lei mais geral. Aceitar isso implica em considerar dois regimes da matéria ou estados de fase do espaço-tempo.

Regime sem auto-gravidade (partículas reais e virtuais)
- intervalo de massa: m < mₒ
- sem fonte de auto-gravidade
- com onda ψ
- com coerência\decoerência

Regime com auto-gravidade (somente partículas reais)
- intervalo de massa: m ≥ mₒ
- com fonte de auto-gravidade
- sem onda ψ
- Os conceitos de coerência\decoerência não se aplicam

      Contrapontos Experimentais Relacionados

● Quanto a auto-gravidade ser detectada em partículas com massa inferior a mₒ

https://www.inovacaotecnologica.com.br/noticias/noticia.php?artigo=torre-pisa-optica-permite-ver-atomos-caindo-20-segundos&id=010165191120#.Xda_CNVKgnR

Fonte
Artigo: Sondando a gravidade segurando átomos por 20 segundos
Autores: Victoria Xu, Matt Jaffe, Cristian D. Panda, Sofus L. Kristensen, Logan W. Clark, Holger Müller
Revista: Science
Vol .: 366 Edição 6466
DOI: 10.1126 / science. aay6428

Até agora as experiências não refutaram nenhum dos argumentos que foram apresentados acima, pois o meu argumento coloca em xeque a auto-gravidade das partículas com massa inferior a mₒ e não a interação gravitacional com átomos. Apesar da proposta interessante da pesquisa, é difícil de determinar experimentalmente se os átomos conseguem gerar um campo gravitacional próprio e ainda não há nada conclusivo nesse sentido.

● Quanto a superposição quântica ser detectada em partículas com massa superior a mₒ

https://hypescience.com/estas-moleculas-gigantes-tambem-seguem-as-bizarras-regras-do-mundo-quantico/

Fonte
https://www.nature.com/articles/s41567-019-0663-9?utm_source=commission_junction&utm_medium=affiliate

Nesse caso também, nenhum dos meus argumentos é refutado, pois a medida que os físicos experimentais tentam detectar superposição quântica para massas cada vez maiores, eles se aproximam pouco a pouco da massa de corte mₒ, mas ainda estão bem distantes.

Até agora a superposição quântica foi observada para moléculas em torno de 25 quilo daltons, mas a massa de corte mₒ é aproximadamente 3.7 exa daltons. Se a mecânica quântica continua a valer além de massas superiores a 3.7 exa daltons (aproximadamente a massa de um grão de poeira) ainda é uma questão a ser respondida no futuro.

Unidades Naturais Normalizadas

Proponho um sistema de unidades naturais inventado por mim, para harmonizar a quantidade de informação, a entropia e suas divergências, com outras medidas dimensionais ordinárias na Física Digital. Neste ensaio, começo a divulgação da minha Teoria Científica situada no âmbito da Física Digital e da Termodinâmica da Gravidade que tem a finalidade de conciliar a Relatividade Geral com a Mecânica Quântica.

Consistência da entropia holográfica no subespaço [LM]

1) Parametrização da Entropia do Buraco Negro

S = A/4Lp²

S = π.r²
Se o raio mínimo r vale Lp, devemos ter
S = π (em unidades de Planck)

Para normalizar a entropia S = 1, para o raio mínimo rₒ, devemos fazer o raio mínimo de um buraco negro valer rₒ = Lp/√π.

Em geral, fazendo r = n.rₒ, obtemos:
S = π.n²rₒ²/π = n²
S = n²

2) Parametrização do Limite de Bekenstein 

A quantidade máxima S de informação oculta numa região de raio r que contém uma massa m é:

Limite de Bekenstein
S ≤ (2π.c/ħ).r.m. (K.ln2)

Interpretação dos cutoffs de massa e raio
mₒ - massa unitária
rₒ   - raio unitário (raio Schwarzschild mínimo)

Identificamos a célula mínima com significado físico no subespaço de fórmulas dimensionais [LM] como sendo o produto das constantes de massa mₒ e de raio rₒ, Sₒ = mₒ.rₒ = ħ/2πc.

Unidade de entropia em [LM]
Sₒ = ħ/2πc = 1

Primeiro parametrizamos as variáveis de raio e massa, como produtos dos cutoffs rₒ e mₒ na expressão usual do limite de Bekenstein. Após esse primeiro passo, abstraímos o K ln 2 da entropia termodinâmica, para obter a expressão da informação I em bits. 

S ≤ (2π.c/ħ).(m.mₒ).(n.rₒ). (K.ln 2)
S ≤ (m.mₒ).(n.rₒ)/(ħ/2πc). (K.ln 2)
S ≤ (m.mₒ).(n.rₒ)/Sₒ . (K.ln 2)
S ≤ mn. mₒ.rₒ/Sₒ . (K.ln 2)
S ≤ mn. Sₒ/Sₒ . (K.ln 2)
S ≤ mn. K ln 2

Sendo a entropia S = K.I.ln 2, obtemos para a informação I:

I = m.n 

número de massa: m = m/mₒ
número do raio:      n = r/rₒ

Os parâmetros numéricos m e n são os números que podem quantizar uniformemente a massa e o raio, do mesmo modo que a informação é quantizada em bits. Adotando essa notação minimalista, podemos identificar mais facilmente os cutoffs de referência de cada dimensão e os intervalos de variação dos observáveis. O que nos faz levar a sério a sugestão de que a divisibilidade infinita (continuidade) é uma ilusão computacional da informação.

Apresentação da base normalizada [LTM]

A parametrização conjunta da entropia do buraco negro (1) e do limite informativo (2) é consistente com a minha proposta para o seguinte sistema de unidades naturais:

rₒ  = Lp/√π = 1
tₒ  = Tp/√π = 1
mₒ = Mp/2.√π = 1

Essas unidades fazem a entropia mínima de Bekenstein coincidir com a entropia do menor buraco negro possível de raio rₒ, normalizando a uma unidade natural de informação (1 bit). Em especial, num horizonte de eventos com m = n, a entropia máxima correspondente é S = n.n = n², que reproduz a informação obtida a partir do princípio holográfico.

Como curiosidade, podemos notar que a velocidade da luz c = rₒ\tₒ, bem como todas as suas potências retornam os mesmos valores numéricos que são obtidos usando as unidades de Planck.

Sobre a entropia das fronteiras holográficas

Muitas vezes, encontramos artigos em revistas especializadas e publicações científicas sobre a termodinâmica dos buracos negros e a gravidade quântica, comentários que confundem a entropia das telas de Planck, definidas como horizontes de eventos estendidos, com o limite de Bekenstein da matéria.

Limite de Bekenstein
S = m.n

Entropia das fronteiras holográficas
I = n²

Com objetos físicos afastados do horizonte de eventos, vale a expressão n ≥ m, o que leva a aparente violação do limite de Bekenstein n² ≥ mn. Entretanto, uma fronteira holográfica não viola o limite de Bekenstein porque inclui todos os processos virtuais que podem existir no bulk, sendo a saturação de entropia n² o esgotamento da entropia na fronteira quando a densidade do bulk se aproxima da densidade crítica μₒ. 

Para qualquer par de coordenadas (n, m) do subespaço [LM], a entropia de Bekenstein é a média geométrica entre m² e n², a saturação em massa e a saturação em espaço: mn = √m²n².

Saturação da entropia em massa
Aumento da densidade inicial μ sem variar a massa m
lim μ -> μₒ (mn); com m = constante e Δn < 0
Estado final: Buraco negro de raio m
Entropia final: mn --> m²

Saturação da entropia em espaço
Aumento da densidade inicial μ sem variar o raio n
lim μ -> μₒ (mn); com n = constante e Δm > 0
Estado final: Buraco negro de raio n
Entropia final: mn --> n²

Resumo mnemônico: Na saturação em massa m², a coordenada n desce até m, na saturação em espaço n², a coordenada m sobe até n.

O Espaço Vetorial de Fórmulas

Na análise dimensional, lidamos muitas vezes com sistemas de equações com duas ou mais variáveis e outros problemas típicos da álgebra linear. Encontramos pouco material na literatura científica que vai além da análise tradicional, na maioria dos casos a declarada inovação se reduz a mera execução dos cálculos no computador.

Entretanto, apresento neste ensaio uma ferramenta heurística que aperfeiçoei como um tipo de "canivete Suíço" para lidar com problemas de análise dimensional, chamada de Espaço Vetorial de Fórmulas.

A Análise Dimensional

A análise dimensional é um método muito utilizado na física teórica para garantir a correção algébrica das fórmulas e para estudar a consistência das novas teorias. A noção mais importante da análise dimensional é a da homogeneidade dimensional ou comensurabilidade, pela qual somente dimensões comensuráveis podem ser comparadas, adicionadas ou subtraídas.

Quantidades de dimensões diferentes são ditas incomensuráveis entre si, isto é, da mesma forma que não podemos somar laranjas com maçãs, não podemos somar Volts com Amperes e nem Watts com Newtons. Desse modo, não faz sentido perguntar se 1 litro é mais, igual ou menos de 1 quilograma, pois estes têm dimensões diferentes, nem somar 1 segundo a 1 metro. Porém, faz todo o sentido perguntar se 1 polegada é mais, o mesmo ou menos de 1 centímetro, pois a mesma dimensão de espaço linear pode ser expressa em unidades diferentes.

O conjunto de todas as fórmulas dimensionais válidas forma um grupo abeliano sob a operação de multiplicação, possibilitando construir novas dimensões apenas multiplicando e dividindo as quantidades incomensuráveis entre si. Á área espaço-temporal ρ, por exemplo, é a quantidade metros x segundos, que se refere ao produto do espaço percorrido pelo tempo de percurso.

As Unidades Naturais de Planck

Chamamos de Unidades Naturais de Planck o sistema baseado no sistema de unidades originalmente proposto por Max Planck em 1899 com o objetivo de simplificar as diversas equações da Física. As cinco constantes físicas fundamentais são G (constante de gravitação universal), ħ (constante reduzida de Planck ou quantum de ação), c (velocidade da luz), a constante de Boltzman Kb e a constante de Coulomb Ke. No presente ensaio, focarei nas três primeiras constantes G, ħ e c. No sistema de unidades naturais, as constantes G, ħ e c ganham o valor 1 (um), eliminando convenientemente qualquer antropocentrismo, pois nesse sistema os resultados numéricos das equações não dependem de nenhuma constante de proporcionalidade.

Introdução ao Espaço Vetorial de Fórmulas

Abordarei nos sub-tópicos destacados abaixo, os conceitos mais importantes para apresentar o Espaço Vetorial de Fórmulas.

● Fórmulas Dimensionais [F]

O físico Percy Williams Bridgman elaborou o teorema central da análise dimensional que afirma que as únicas funções que podem ter argumentos dimensionais são produtos de potências das grandezas de base de um determinado sistema de unidades.

[F] = [L]^x.[T]^y.[M]^z    
 F  ↔ V (x, y, z)   

Definimos o espaço vetorial de fórmulas da base [LTM] como o conjunto de todas as suas fórmulas dimensionais válidas [F], cuja representação vetorial forma um espaço Euclidiano em R³.

Nesse formalismo, mapeamos cada expressão algébrica F para seu respectivo vetor V por intermédio de sua fórmula dimensional [F].

● A Base Canônica [LTM]

Indo além, percebemos que [L], [T] e [M] são melhor expressos em unidades naturais de Lp (comprimento de Planck), Tp (tempo de Planck) e Mp (massa de Planck). Isso significa que através da base canônica de Planck podemos traduzir todas as fórmulas da física para quaisquer bases alternativas que desejarmos.

● A Base das Constantes Físicas [Għc]

Como vimos no ensaio anterior, as três constantes fundamentais da Física são importantes porque substituem formalmente os três vetores da base canônica de Planck. Utilizando essas constantes podemos representar quaisquer dimensões, bem como inferir alguns cutoffs dos observáveis físicos.

Representação dos vetores da base [Għc]
Vetor de [G] = (3, -2, -1)
Vetor de  [ħ] = (2, -1, 1)
Vetor de  [c] = (1, -1, 0)

● Equações e operações básicas

Na base canônica [LTM], cada fórmula dimensional é representada por um vetor e a equivalência entre duas representações do mesmo vetor em bases diferentes representa uma equação. Assim, de modo compacto e elegante, a maioria das equações da Física podem ser lidas e interpretadas no âmbito do espaço vetorial de fórmulas através dos seus vetores-fórmulas correspondentes.

Exemplo:
E      = (2, -2, 1)
M.c² = (0, 0, 1) + (2, -2, 0)

|Entidades matemáticas|  |                Equações                  |
|              Vetores             |  |  (2, -2, 1) = (0, 0, 1) + (2, -2, 0) |         
|             Fórmulas           |  |             E = M.c²                        |      

Nessa codificação, a operação de multiplicação de dimensões (x) é representada pela soma vetorial "+" e a operação de divisão de dimensões (:) é representada pela subtração vetorial "-".

● Representação de magnitudes

Magnitudes específicas também podem ser construídas facilmente, bastando incluir um multiplicador de normalização. A Energia é representada pelo vetor V = (2, -2, 1) em [LTM], cujo módulo euclidiano é ||V||=3, assim W = 5\3 (2, -2, 1) tem magnitude 5.

Portanto, o vetor W pode representar 5 Joules na base [metro, segundo, quilograma] ou pode representar 5 unidades de energia de Planck se preferirmos utilizar a base das unidades naturais [Lp, Tp, Mp].

● Análise dimensional em subespaços
Mecânica Quântica no subespaço [LT]

Tratando a massa como uma grandeza adimensional em todas as fórmulas podemos estudar os fenômenos quânticos sem mencionar a massa explicitamente.

Constante de ação em [LT]
[ħ\mₒ] = (2,-1,0)

Que lemos como "constante reduzida de Planck por massa".

● Um upgrade da análise dimensional tradicional

A utilização do espaço [LTM] para representar as equações da Física é uma ferramenta heurística poderosa, possibilitando automatizar procedimentos para classificação de dados e implementar inteligência artificial para estudar a natureza.

Além das ferramentas tradicionais da álgebra linear, a visualização das fórmulas no espaço geométrico permite um ataque mais efetivo aos mais diversos problemas da Física, especialmente no que tange a acomodação de novas teorias dentro do arcabouço científico vigente.

As Constantes Fundamentais da Física

Constantes naturais são essenciais para a física teórica, nos revelando uma estrutura subjacente que possui sua própria linguagem característica. Números adimensionais e dimensões se combinam como numa "Biblioteca de Babel" com uma estrutura extremamente rica que só pode ser vislumbrada num espaço vetorial de fórmulas abstratas.

Quantas são as constantes fundamentais do universo?

Michael Duff, num artigo científico provocativo "Trialogue on the Number of Fundamental Constants" (link no final) disse que não acredita em nenhum número de constantes fundamentais. O motivo apresentado por ele é que as constantes dimensionais não independem do sistema de medidas adotado, portanto não seriam as "verdadeiras" constantes.

Na conclusão do referido artigo ele sugere que enquanto a noção de constantes fundamentais não for esclarecida, a polêmica vai continuar. Concordo plenamente que nunca é pedir demais por debates que possam esclarecer as coisas sobre um conteúdo tão importante. No meu entendimento o artigo científico é muito bom. Porém, é evidente que Michael Duff visa um tópico diferente do título do artigo que trata da determinação do número de constantes fundamentais, um assunto que não foi sequer abordado tangencialmente pelos seus colegas do triálogo Lev B. Okun e Gabriele Veneziano.

Segundo Duff, um universo com constantes dimensionais alteradas seria indistinguível do nosso universo, um argumento que vai contra o pensamento do cientista George Gamow, expresso na sua série de livros de divulgação científica do Sr. Tompkins. Michael Duff está correto em destacar que as constantes adimensionais contém informação privilegiada sobre nosso universo, mas está equivocado em desprezar as constantes dimensionais como irrelevantes para a Física.

Uma constante é fundamental, a grosso modo e do ponto de vista utilitário, se ela aparecer mais do que as outras concorrentes na maioria dos livros didáticos de Física, revistas e artigos científicos. E as constantes G, ħ e c, cumprem bem esse requisito.

Se dependesse somente desse argumento utilitarista ou alguma adaptação bem elaborada dele, o cientista russo Lev B. Okun, partidário das três constantes fundamentais, seria o vencedor do debate.

Unidades Básicas de Planck

A expressão constante fundamental pode significar muitas coisas diferentes; valores numéricos que valem em todos os lugares e épocas, valores que são imprescindíveis para a Física Teórica, valores que não mudam conforme as arbitrariedades humanas e etc. Além disso, ainda há uma sobreposição entre os diversos significados, o que acrescenta mais dificuldade a esse estudo semântico difícil. No argumento mais tradicional, apresentado por Lev Okun, os sistemas métricos e as unidades naturais determinam o que pode e o que não pode ser considerado fundamental na Física. Para esse cientista, a constante de gravitação G, a constante de momento angular ħ e a constante da velocidade da luz c, são as três constantes fundamentais do universo.

O argumento detalhado envolve o Teorema de Bridgman que prova que três dimensões métricas bastam para construir todas as outras. No sistema internacional de unidades, essas unidades métricas são o metro para medir o espaço, o quilograma para medir a massa e o segundo para medir o tempo, o velho MKS do ensino médio. Como numa montagem com os blocos de montar Lego, todas as dimensões da natureza são obtidas através de três tipos de "Legos" básicos: O Metro, o Quilograma e o Segundo.

A distinção entre as unidades primitivas e as unidades derivadas, separa naturalmente na intuição o que é primitivo do que pode ser derivado dos primitivos. Em última análise, a convicção intuitiva que nós temos de que a base dos vetores deve ser fundamental só expressa a matemática do espaço vetorial. Para a maioria, essa definição de constante fundamental basta para todos os propósitos práticos, sendo que os radicais do partido das três constantes usariam as unidades básicas de Planck Lp, Tp e Mp, como as três constantes fundamentais, ao invés das constantes experimentais G, ħ e c.

O comprimento de Planck Lp, o Tempo de Planck Tp e a Massa de Planck Mp, são imprescindíveis para a Física porque seguem rigorosamente o teorema de Bridgman e formam uma base ortonormal no espaço vetorial de fórmulas dimensionais. Em contraste, as constantes G, ħ e c são apenas uma base não ortogonal de fórmulas, cuja correspondência com outras grandezas físicas de referência em algum sistema de unidades é obtida através das unidades naturais apropriadas. Ou seja, toda física que podemos fazer com G, ħ e c, pode ser feita de forma ainda mais eficiente com Lp, Tp e Mp.

Comprimento de Planck
Lp = 1.616 x 10^-35 metros
0.00000000000000000000000000000000001616 m

Tempo de Planck
Tp= 5.400 x 10^-44 segundos
0.000000000000000000000000000000000000000000054 s

Massa de Planck
Mp= 2.176 x 10^-8 quilogramas
0.00000002176 Kg

As constantes fundamentais como cutoffs dos observáveis físicos

Superficialmente, as constantes dimensionais podem ser interpretadas como fatores de conversão, mas quanto a isso estou em sintonia com o argumento de Veneziano.

O que torna uma constante especial, além de mero fator de conversão entre dimensões, é a sua relevância num universo finito que apresenta intervalos válidos com cutoffs dos observáveis. Seja um cutoff máximo ou mínimo da natureza, todos os valores que uma dimensão pode exibir dependem dos respectivos cutoffs, independente da utilidade dos mesmos como fatores de conversão.

Logo, a proposição lógica que esclarece e ataca diretamente o problema semântico das constantes fundamentais da Física e que generaliza o comentário sagaz de Veneziano no debate é:

● Todas as constantes fundamentais podem ser utilizadas como fatores de conversão, mas nem todos os fatores de conversão podem ser constantes fundamentais.

Constantes dimensionais x adimensionais

A informação sui generis de uma constante adimensional, que não muda de valor com a mudança deliberada do sistema de medida, assim como a constante de estrutura fina α, talvez nos indique alguma grandeza importante que não prestamos a devida atenção. Pela própria consistência das ferramentas matemáticas utilizadas na física teórica, as unidades adimensionais tabeladas nada mais são do que projeções de números num eixo adimensional comum que é ortogonal aos eixos das dimensões conhecidas.

Enquanto existirem relações matemáticas inexplicadas entre as diversas constantes que se projetam de forma adimensional, permanece a possibilidade de que algumas delas se refiram a dimensões ausentes e não identificadas numa primeira análise. É um raciocínio circular defender a primazia das constantes adimensionais, para logo em seguida priorizar as constantes dimensionais na leitura e interpretação dos valores adimensionais. Concordo com Michael Duff quanto a relevância das constantes adimensionais, mas por um motivo diferente do considerado por ele (de serem as verdadeiras constantes), elas são importantes porque revelam relações profundas entre as dimensões e os valores adimensionais.

No meu entendimento o universo pode guardar de forma críptica os seus segredos nas bases de representação do espaço de fórmulas dimensionais. Estudando as bases menos comuns, rotacionando e concatenando as dimensões podemos enxergar o que não poderíamos ter visto numa outra base de representação mais trivial.

Texto de referência com link (arXiv):

Trialogue on the Number of Fundamental Constants